2진수, 4진수, 8진수, 16진수의 차이와 변환 방법 (완벽 가이드)

컴퓨터는 기본적으로 **이진수(2진수)**를 사용하여 데이터를 처리합니다. 그러나 2진수뿐만 아니라 4진수, 8진수, 16진수도 프로그래밍과 컴퓨터 시스템에서 자주 사용됩니다. 이 글에서는 각 진수의 개념과 사용 방법, 그리고 서로 다른 진수 간의 변환 과정을 다루어보겠습니다.
2진수 (Binary)란?
2진수(Binary)는 컴퓨터 시스템의 기본 수 체계로, 0과 1 두 개의 숫자만 사용합니다. 컴퓨터의 모든 데이터는 이 두 숫자를 통해 처리됩니다. 이는 전기 신호의 ON(1)과 OFF(0) 상태를 나타내기 때문에 컴퓨터가 데이터를 처리하는 데 가장 효율적인 방식입니다.
예시)
10진수 100을 2진수로 변환하면 1100100입니다.
변환 과정은 다음과 같습니다:
- 100 ÷ 2 = 50, 나머지: 0
- 50 ÷ 2 = 25, 나머지: 0
- 25 ÷ 2 = 12, 나머지: 1
- 12 ÷ 2 = 6, 나머지: 0
- 6 ÷ 2 = 3, 나머지: 0
- 3 ÷ 2 = 1, 나머지: 1
- 1 ÷ 2 = 0, 나머지: 1
결과: 1100100
4진수 (Quaternary)란?
4진수(Quaternary)는 숫자 0부터 3까지를 사용하여 값을 표현하는 진법입니다. 4진수는 주로 특정 프로그래밍 언어의 데이터 표현 방식이나 알고리즘에서 사용되며, 2진수보다 간결하게 데이터를 표현할 수 있습니다.
예시)
10진수 100을 4진수로 변환하면 1210입니다.
변환 과정은 다음과 같습니다:
- 100 ÷ 4 = 25, 나머지: 0
- 25 ÷ 4 = 6, 나머지: 1
- 6 ÷ 4 = 1, 나머지: 2
- 1 ÷ 4 = 0, 나머지: 1
결과: 1210
8진수 (Octal)란?
8진수(Octal)는 숫자 0부터 7까지를 사용합니다. 8진수는 과거 컴퓨터 시스템에서 많이 사용되었으며, 특히 데이터 압축 및 저장에 유용합니다. 2진수보다 압축된 형태로 데이터를 표현할 수 있으며, 16진수보다 읽기 쉽습니다.
예시)
10진수 100을 8진수로 변환하면 144입니다.
변환 과정은 다음과 같습니다:
- 100 ÷ 8 = 12, 나머지: 4
- 12 ÷ 8 = 1, 나머지: 4
- 1 ÷ 8 = 0, 나머지: 1
결과: 144
16진수 (Hexadecimal)란?
16진수(Hexadecimal)는 0부터 9까지의 숫자와, A(10), B(11), C(12), D(13), E(14), F(15)까지의 알파벳을 사용하여 데이터를 표현합니다. 16진수는 2진수보다 훨씬 간결하게 데이터를 표현할 수 있어, 메모리 주소나 프로그래밍에서 자주 사용됩니다.
예시)
10진수 100을 16진수로 변환하면 64입니다.
변환 과정은 다음과 같습니다:
- 100 ÷ 16 = 6, 나머지: 4
- 6 ÷ 16 = 0, 나머지: 6
결과: 64
※ 진수 변환 표
다음은 10진수, 2진수, 4진수, 8진수, 16진수의 기본 변환 표입니다:
| 10진수 | 2진수 | 4진수 | 8진수 | 16진수 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 | 2 |
| 3 | 11 | 3 | 3 | 3 |
| 4 | 100 | 10 | 4 | 4 |
| 5 | 101 | 11 | 5 | 5 |
| 6 | 110 | 12 | 6 | 6 |
| 7 | 111 | 13 | 7 | 7 |
| 8 | 1000 | 20 | 10 | 8 |
| 9 | 1001 | 21 | 11 | 9 |
| 10 | 1010 | 22 | 12 | A |
| 11 | 1011 | 23 | 13 | B |
| 12 | 1100 | 30 | 14 | C |
| 13 | 1101 | 31 | 15 | D |
| 14 | 1110 | 32 | 16 | E |
| 15 | 1111 | 33 | 17 | F |
진수 변환 방법
- 2진수로 변환하는 방법
- 2진수로 변환하는 방법은 숫자를 2로 나누어 몫과 나머지를 계산하는 것입니다. 몫이 0이 될 때까지 반복하며 나머지들을 기록하고, 거꾸로 나열하면 2진수가 됩니다.
- 4진수로 변환하는 방법
- 4진수로 변환할 때는 숫자를 4로 나누어 몫과 나머지를 계산합니다. 몫이 0이 될 때까지 반복하며 나머지들을 기록합니다. 마지막에 나머지들을 거꾸로 나열하면 4진수 값을 얻을 수 있습니다.
- 8진수로 변환하는 방법
- 8진수는 숫자를 8로 나누어 몫과 나머지를 계산한 후 나머지를 기록합니다. 몫이 0이 될 때까지 이 과정을 반복합니다. 마지막으로 나머지들을 거꾸로 나열하면 8진수가 됩니다.
- 16진수로 변환하는 방법
- 16진수로 변환하는 과정은 16으로 나누어 몫과 나머지를 계산하는 방식입니다. 나머지가 10 이상일 경우, 해당 숫자를 A, B, C, D, E, F로 변환하여 표시합니다. 마찬가지로, 나머지를 거꾸로 나열하면 16진수가 됩니다.
진수가 사용되는 이유
- 2진수: 컴퓨터의 기본적인 수 체계로, 데이터의 저장과 처리에 사용됩니다.
- 4진수: 주로 알고리즘이나 특정 데이터 구조에서 사용되며, 2진수보다 조금 더 압축된 데이터를 표현할 수 있습니다.
- 8진수: 과거의 시스템에서 많이 사용되었으며, 지금도 간결한 표현이 필요할 때 쓰입니다.
- 16진수: 주로 메모리 주소, 색상 코드, 디버깅 등에 자주 사용됩니다. 특히 프로그래머와 시스템 관리자에게 유용한 진수입니다.
결론
2진수, 4진수, 8진수, 16진수는 모두 컴퓨터 시스템에서 중요한 역할을 합니다. 각 진수는 데이터 표현의 효율성과 가독성을 높이기 위해 사용되며, 프로그래머와 시스템 관리자들이 데이터를 쉽게 관리하고 처리할 수 있도록 돕습니다. 이 글에서 소개한 진수 변환 방법을 통해, 다양한 진법을 이해하고 실생활에서 활용할 수 있을 것입니다.
※ 진수 변환 파이썬 코드
# 10진수를 입력 받아 2진수, 4진수, 8진수, 16진수로 변환하는 함수
def convert_base(number):
print(f"10진수: {number}")
# 2진수로 변환 (bin() 함수는 '0b' 접두사를 붙여서 반환)
binary = bin(number)[2:] # 접두사 '0b' 제거
print(f"2진수: {binary}")
# 4진수로 변환
def dec_to_base4(n):
if n == 0:
return "0"
base4 = ""
while n > 0:
base4 = str(n % 4) + base4
n //= 4
return base4
base4 = dec_to_base4(number)
print(f"4진수: {base4}")
# 8진수로 변환 (oct() 함수는 '0o' 접두사를 붙여서 반환)
octal = oct(number)[2:] # 접두사 '0o' 제거
print(f"8진수: {octal}")
# 16진수로 변환 (hex() 함수는 '0x' 접두사를 붙여서 반환)
hexadecimal = hex(number)[2:].upper() # 접두사 '0x' 제거, 대문자로 출력
print(f"16진수: {hexadecimal}")
# 예시로 46655를 변환
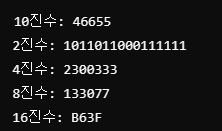
convert_base(46655)
결과값
8진수를 16진수로 변환하는 방법: 10진수 및 2진수를 거치는 방법
8진수를 16진수로 변환하는 방법: 10진수 및 2진수를 거치는 방법8진수를 16진수로 변환하는 방법에는 여러 가지가 있습니다. 이 글에서는 두 가지 방법, 즉 10진수를 거치는 방법과 2진수를 거치는
honeyjuny.tistory.com
'IT' 카테고리의 다른 글
| 8진수를 16진수로 변환하는 방법: 10진수 및 2진수를 거치는 방법 (0) | 2024.10.21 |
|---|---|
| SQL Server 교착 상태(Deadlock) 발생 및 해결 방법 / 트랜잭션이 잠금 리소스에서 다른 프로세스와의 교착 상태가 발생하여 실행이 중지되었습니다. (0) | 2024.10.16 |
| C#에서 문자열을 연결할 때 StringBuild가 + 연산자보다 훨씬 빠르다. (0) | 2024.06.24 |
| 오픈소스 Chart 라이브러리 정리 (1) | 2024.04.01 |
| GPS(Global Positioning System)에 대해서 알아보자. (0) | 2023.05.17 |